![]() __________
__________
专题13 圆的有关地方关系

![]()
【考试知识点1】点与圆的地方关系
【例1】(2018·浙江中考考试真题)用反证法证明时,假设结论“点在圆外”不成立,那样点与圆的地方关系只能是( )
A.点在圆内 B.点在圆上 C.点在圆心上 D.点在圆上或圆内
【答案】D
【分析】【剖析】在假设结论不成立时应该注意考虑结论的反面所大概的状况,假如只有一种,那样否定一种就能了,假如有多种状况,则需要一一否定.
【解答】用反证法证明时,假设结论“点在圆外”不成立,
那样点应该在圆内或者圆上.
故选D.
【点评】考查反证法与点和圆的地方关系,解题的重点是学会点和圆的地方关系.
【变式1-1】(2016·湖北中考考试真题)在公园的O处附近有E、F、G、H四棵树,地方如图所示(图中小正方形为边长均相等),现计划修建一座以O为圆心,OA为半径的圆形水池,需要池中不留树木,则E、F、G、H四棵树中需要被移除的为()

A.E、F、G B.F、G、H C.G、H、E D.H、E、F
【答案】A
【分析】
考试试题剖析:依据圆与直线的地方关系可得:点E、F、G在圆内,点H在圆外.
考试知识点:点与圆的地方关系
【变式1-2】(2017·山东中考考试真题)如图,在网格(每一个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),假如以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【分析】
考试试题剖析:给各点标上字母,如图所示.
AB=![]() =
=![]() ,AC=AD=
,AC=AD=![]() =
=![]() ,AE=
,AE=![]() =
=![]() ,AF=
,AF=![]() =
=![]() ,AG=AM=AN=
,AG=AM=AN=![]() =5,∴
=5,∴![]() 时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.故选B.
时,以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.故选B.
考试知识点:点与圆的地方关系;勾股定理;推理填空题.
【考试知识点2】直线与圆的地方关系
【例2】(2018·黑龙江中考考试真题)已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
【答案】0
【分析】
【剖析】借助待定系数法得出直线分析式,再得出平移后得到的直线,求与坐标轴交点的坐标,转化为直角三角形中的问题,再由直线与圆的地方关系的断定解答.
【解析】把点(12,﹣5)代入直线y=kx得,
﹣5=12k,
∴k=﹣![]() ;
;
由y=﹣![]() x平移m(m>0)个单位后得到的直线l所对应的函数关系式为y=﹣
x平移m(m>0)个单位后得到的直线l所对应的函数关系式为y=﹣![]() x+m(m>0),
x+m(m>0),
设直线l与x轴、y轴分别交于点A、B,(如图所示)
当x=0时,y=m;当y=0时,x=![]() m,
m,
∴A(![]() m,0),B(0,m),
m,0),B(0,m),
即OA=![]() m,OB=m,
m,OB=m,
在Rt△OAB中,AB=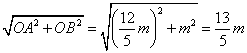 ,
,
过点O作OD⊥AB于D,
∵S△ABO=![]() OD•AB=
OD•AB=![]() OA•OB,
OA•OB,
∴![]() OD•
OD•![]() =
=![]() ×
×![]() m×m,
m×m,
∵m>0,解得OD=![]() m,
m,
由直线与圆的地方关系可知![]() m <6,解得m<
m <6,解得m<![]() ,
,
故答案为0
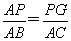
【点睛】本题考查了直线的平移、直线与圆的地方关系等,可以用含m的式子表示出原点到平移后的直线的距离是解题的重点.本题有肯定的困难程度,借助数形结合思想进行解答比较直观明了.
【变式2-1】(2019·广东中考考试真题)平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )
A.0条 B.1条 C.2条 D.无数条
【答案】C
【分析】
【剖析】
第一判断点与圆的关系,然后再剖析P可作⊙O的切线条数即可解答.
【解析】
解:由于点P到O的距离为2,大于半径1,所以点P在圆外,
所以,过点P可作⊙O的切线有2条;
故选C.
【点睛】
本题考查了点与圆的关系、切线的概念,熟练学会是解题的重点.
【变式2-2】(2019·浙江中考考试真题)如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上一动点,当半径为6的圆
上一动点,当半径为6的圆![]() 与
与![]() 的一边相切时,
的一边相切时,![]() 的长为________.
的长为________.
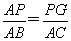
【答案】![]() 或
或![]()
【分析】
【剖析】
依据勾股定理得到![]() ,
,![]() ,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,当⊙P于AB相切时,点P到AB的距离=6,依据相似三角形的性质即可得到结论.
,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,当⊙P于AB相切时,点P到AB的距离=6,依据相似三角形的性质即可得到结论.
【解析】
∵在Rt△ABC中,∠C=90°,AC=12,BD+CD=18,
∴![]() ,
,
在Rt△ADC中,∠C=90°,AC=12,CD=5,
∴![]() ,
,
当⊙P于BC相切时,点P到BC的距离=6,
过P作PH⊥BC于H,则PH=6,
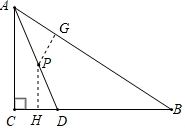
∵∠C=90°,
∴AC⊥BC,
∴PH∥AC,
∴△DPH∽△DAC,
∴![]() ,
,
∴![]() ,
,
∴PD=6.5,
∴AP=6.5;
当⊙P于AB相切时,点P到AB的距离=6,
过P作PG⊥AB于G,
则PG=6,
∵AD=BD=13,
∴∠PAG=∠B,
∵∠AGP=∠C=90°,
∴△AGP∽△BCA,
∴![]() ,
,
∴![]() ,
,
∴AP=3![]() ,
,
∵CD=5<6,
∴半径为6的⊙P不与△ABC的AC边相切,
综上所述,AP的长为6.5或3![]() ,
,
故答案为6.5或3![]() .
.
【点睛】
本题考查了切线的断定和性质,勾股定理,相似三角形的断定和性质,熟练正确切线的性质是解题的重点.






